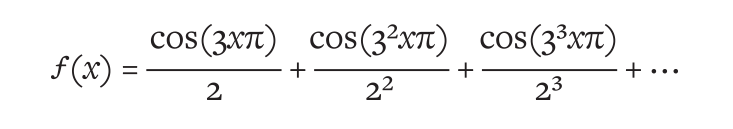Bruno’s Dream I*
The universe is then one, infinite, immobile....
Giordano Bruno (1548-1600) was a Dominican friar tortured to death by the Catholic Church for having this dream (and then telling people about it):
‘The universe is then one, infinite, immobile…. It is not capable of comprehension and therefore is endless and limitless, and to that extent infinite and indeterminable, and consequently immobile.’
~Teofilo, in Cause, Principle, and Unity, Fifth Dialogue, (1588)
His vision proved correct; scientists think it was a lucky guess.
Commentary:
Of Bruno’s Coincidentia Oppositorum, James Joyce wrote that it is ‘[…] a kind of dualism—every power in nature must evolve an opposite in order to realise itself and opposition brings reunion.’
In Finnegans Wake, there are numerous allusions to Bruno, including his trial, torture and murder. Pun-lover Joyce plays upon Coincidentia Oppositorum with fictional Dublin publisher, “Browne and Nolan” and “brownesberrow in nolandsland.”
This from Adam Kurcharsky in Math’s Beautiful Monster, Nautilus: ‘In 1904, Albert Einstein introduced physicists to the idea of “Brownian motion”: Particles in a liquid, he said, follow a random path because fluid molecules are constantly knocking them around. The collisions are so frequent (more than 1021 per second) that no matter how good the microscope, or how detailed the observation, the trajectories are never smooth. At the practical level, it is not possible to find a derivative. If researchers wanted to work with such problems, they would need to confront Weierstrass’ monster**—and that is exactly what Einstein did. His theory for Brownian motion used functions that were infinitely jagged. It set a longstanding precedent: Physicists have used non-smooth functions as a proxy for Brownian motion ever since.’
*Iris Murdoch wrote Bruno’s Dream about a dying arachnophile. See Dream 4628, Bruno’s Dream II.
**German mathematician who, in 1872, gave birth to the monster which expresses a function both continuous and not smooth at any point (thereby challenging the foundations calculus):